Mode Interactions in
Spherical Rayleigh-Bénard Convection
In the fluid layer between a hot and cold spherical shell, changes to the width and temperature gradient can modify the number of convection cells present. Although a vast simplification, this model is analogous to the earth’s atmosphere where the convection pattern influences the latitudinal low and high pressure zones. In the paper a simplified ODE model is used to understand this behaviour.
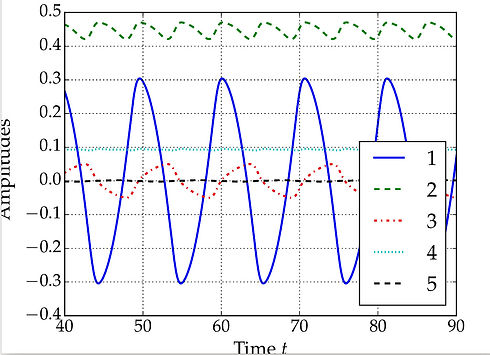
Animation Left: As the temperature gradient is increased across the a time-periodic solution emerges. The spherical geometry constrains even & odd modes to oscillate with a 2:1 frequency ratio.
Shown in the following pages are the (l=1,m=3), (l=2,m=4) oscillations.
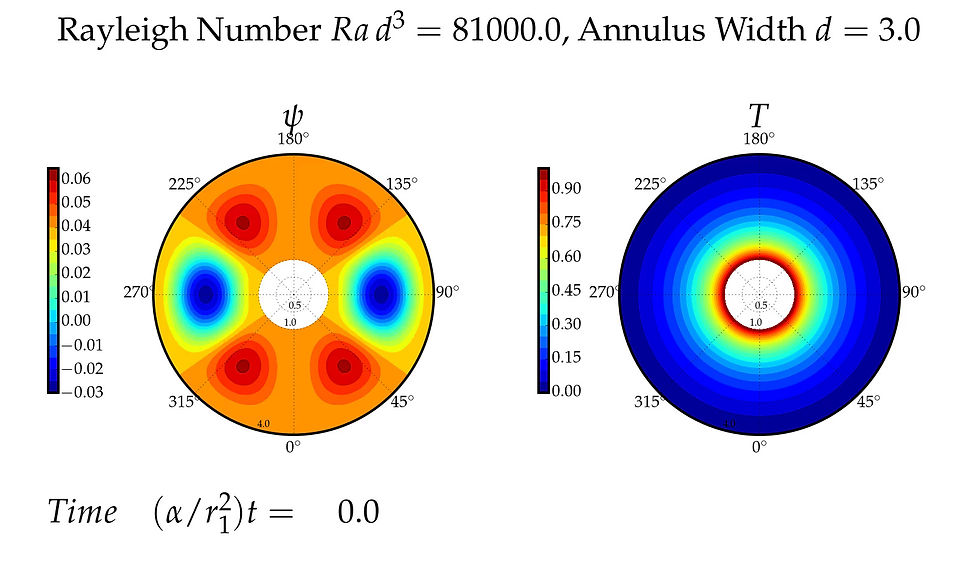
l=1,m-3 Oscillation
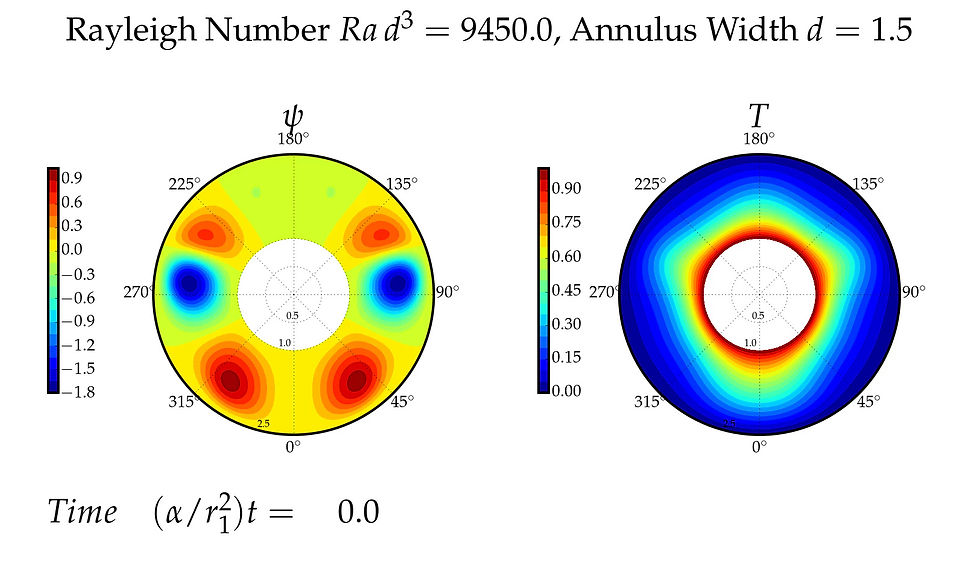
l=2,m=4 Oscillation
Understanding hysteretic transitions in fluid flows
Bistability and hysteresis of thermal convection between differentially rotating
spheres pdf preprint
Bistability occurs when two stable states are equally favourable. The underlying system has Hysteresis when the chosen state depends on the systems history. As shown in the image left, the preferred state need not maximise heat transfer and it depends on how the temperature gradient is changed.
The understanding of tipping points, regime shifts and species collapse are understood using related ideas to bistability and hysteresis.
Studying a model of thermal convection between differentially rotating spheres, we find that this behaviour is prevalent when the systems state. For example when the system jumps from a convection dominated state favouring heat transfer to a rotation dominated state favouring momentum transfer.
Our results demonstrate that although bistability in this system cannot be simply explained by the flow maximising its torque or heat transfer, the polar and equatorial regions are of particular significance.


